背景
阅读LIC-fusion论文的过程中的一些公式的推导。
State Vector
\(x = [x_I^\top, x_{\text{calib\_C}}^\top, x_{\text{calib\_L}}^\top, x_C^\top, x_L^\top]\) where \(\begin{aligned} x_{I} &= [^{I_{k}}_G \overline{q}^\top,b_{g}^\top,^G v_{I_{k}}^\top,b_{a}^\top,^Gp_{I_{k}}^\top] \\ x_C &= [^{I_{a_{1}}}_G\overline{q}^\top, ^Gp_{I_{a_{1}}}^\top \cdots ^{I_{a_{m}}}_G\overline{q}^\top, ^Gp_{I_{a_{m}}}^\top] \\ x_L &= [^{I_{b_{1}}}_G\overline{q}^\top, ^Gp_{I_{b_{1}}}^\top \cdots ^{I_{b_{n}}}_G\overline{q}^\top, ^Gp_{I_{b_{n}}}^\top] \\ \end{aligned}\)
注意到,在LIC Fusion的状态向量的定义中,相机与激光雷达的状态不再是相机与激光雷达的旋转与平移,而是其自身时间戳下的IMU的旋转与平移。
State Propagation
以新来一帧激光雷达的数据为例: New cloned LiDAR state estimate:
\[\hat{x}_{L_k}(\hat{t}_{I_k}) = [^{I_k}_G \hat{\overline{q}}(\hat{t}_{I_K})^\top, ^G\hat{p}_{I_k}(\hat{t}_{I_k})^\top]\]The augmented covariance matrix is:
\[\begin{bmatrix} P(\hat{t}_{I_{k}}) && P(\hat{t}_{I_{k}})J_{I_{k}}(\hat{t}_{I_{k}})^\top \\ J_{I_{k}}(\hat{t}_{I_{k}})P(\hat{t}_{I_{k}}) && J_{I_{k}}(\hat{t}_{I_{k}})P(\hat{t}_{I_{k}})J_{I_{k}}(\hat{t}_{I_{k}})^\top) \end{bmatrix}\]where $J_{I_{k}}(\hat{t}{I{k}})$ is the jacobian of the new cloned $\hat{x}{L{k}}(\hat{t}{I{k}})$ with respect to the current state.
\[J_{I_{k}} (\hat{t}_{I_{k}}) = \frac{\partial \delta x_{L_{k}} (\hat{t}_{I_{k}})}{\partial \delta x} =[J_I, J_{\text{calib\_C}}, J_{\text{calib\_L}}, J_{C}, J_L]\]derivation of $J_I$
因为Lidar的state vector就是自身时间戳的IMU的位姿,显然有:
\[J_{I} = \begin{bmatrix} I_{3\times3} && 0_{3\times 9} && 0_{3\times 3} \\ 0_{3\times 3} && 0_{3\times_9} && I_{3\times 3} \end{bmatrix}\]derivation of $J_{\text{calib_C}}$,$J_C$,$J_L$
Lidar 的state vector相对于相机的外参以及其他时刻的相机与雷达的state无关,故都设为0。
derivation of $J_{\text{calib_L}}$
\(\begin{aligned} ^{I_{k}}_{G}R(t_{I_{k}} + \tilde{t}_{dL})&= \exp ([\hat\omega_{t_{I_{k}}} \tilde{t}_{dL}]_\times)R(t_{I_{k}}) \\ \implies \exp ([\delta \theta]_\times)^{I_{k}}_{G}R(t_{I_{k}}) &= \exp ([\hat\omega_{t_{I_{k}}} \tilde{t}_{dL}]_\times)R(t_{I_{k}}) \\ \implies \delta \theta &= \hat\omega_{t_{I_{k}}} \tilde{t}_{dL} \\ \implies \frac{\partial \delta \theta}{\partial \tilde{t}_{dL}} &= \hat\omega_{t_{I_{k}}} \\ \end{aligned}\)
\[\begin{aligned} p(t_{L} + \hat{t}_{dL} + \tilde{t}_{dL}) &= p(t_{L} + \hat{t}_{dL}) +\hat{v}({t_L+\hat{t}_{dL}})\tilde{t}_{dL} \\ \implies \hat{p} + \tilde{p} &= \hat{p} + \hat{v}({t_L+\hat{t}_{dL}})\tilde{t}_{dL} \\ \implies \tilde{p} &= \hat{v}({t_L+\hat{t}_{dL}})\tilde{t}_{dL}\\ \implies \frac{\partial \tilde{p}}{\partial \tilde{t}_{dL}} &= \hat{v}_{t_{I_{k}}}\\ \end{aligned}\]Measurement Models
r的左半部分
引子
参照Jianhao Jiao在”Greedy-Based Feature Selection for Efficient LiDAR SLAM”的补充材料中提到的证明方法,首先给出两个公式$r\times s = [r]_\times s$以及
\[\frac{\partial }{\partial x} \|x\| = \frac{x}{\|x\|}\]Let \(y = \| (p' - p_1)\times (p' - p_2)\|\) then \(\begin{aligned} \frac{\partial r_e}{\partial t_K} &= \frac{\partial r_{e}}{\partial y} \frac{\partial y}{\partial p'}\frac{\partial p'}{\partial t_{K}} \\ \end{aligned}\)
where \(\begin{aligned} \frac{\partial r_{e}}{\partial y} &= \frac{1}{\|p_1-p_2\|} \\ \frac{\partial y}{\partial p'} &= \frac{\partial y}{\partial ((p' - p_1)\times (p' - p_2))} \frac{\partial ((p' - p_1)\times (p' - p_2))}{\partial p'} \\ &= \frac{((p' - p_1)\times (p' - p_2))}{\|((p' - p_1)\times (p' - p_2))\|} [p_2-p_1]_\times\\ \frac{\partial p'}{\partial t_{K}} &= I \\ \end{aligned}\)
therefore, \(\frac{\partial r_{e}}{\partial t_{K}} = \frac{1}{\|p_1-p_2\|} \frac{((p' - p_1)\times (p' - p_2))}{\|((p' - p_1)\times (p' - p_2))\|} [p_2-p_1]_\times\)
那么在LIC-fusion中:
令 \(y = \| (^{L_{l}}p_{fi} - ^{L_{l}}p_{fj})\times (^{L_{l}}p_{fi} - ^{L_{l}}p_{fk})\|_2\) 则有 \(\begin{aligned} \frac{\partial \delta r(^L_{l+1}p_{f_{i}})}{\partial ^{L_l} \delta p_{f_{i}}} &= \frac{\partial r(^{L_{l+1}}p_{f_i})}{\partial ^{L_l}p_{f_{i}}} = \frac{\partial r(^{L_{l+1}}p_{f_i})}{\partial y}\frac{\partial y}{\partial ^{L_l}p_{f_{i}}} \end{aligned}\) 并且 \(\begin{aligned} \frac{\partial r(^{L_{l+1}}p_{f_i})}{\partial y} &= \frac{1}{ \|^{L_{l}}p_{fk} - ^{L_{l}}p_{fj}\|_2} \\ \frac{\partial y}{\partial ^{L_l}p_{f_{i}}} &= \frac{ (^{L_{l}}p_{fi} - ^{L_{l}}p_{fj})\times (^{L_{l}}p_{fi} - ^{L_{l}}p_{fk}) }{\| (^{L_{l}}p_{fi} - ^{L_{l}}p_{fj})\times (^{L_{l}}p_{fi} - ^{L_{l}}p_{fk})\|_2 } [^{L_{l}}p_{fk} - ^{L_{l}}p_{fj})]_\times \end{aligned}\) 所以 \(\frac{\partial \delta r(^L_{l+1}p_{f_{i}})}{\partial ^{L_l} \delta p_{f_{i}}} = \frac{1}{ \|^{L_{l}}p_{fk} - ^{L_{l}}p_{fj}\|_2} \frac{ (^{L_{l}}p_{fi} - ^{L_{l}}p_{fj})\times (^{L_{l}}p_{fi} - ^{L_{l}}p_{fk}) }{\| (^{L_{l}}p_{fi} - ^{L_{l}}p_{fj})\times (^{L_{l}}p_{fi} - ^{L_{l}}p_{fk})\|_2 } [^{L_{l}}p_{fk} - ^{L_{l}}p_{fj})]_\times\)
r的右半边
首先给出关系式
\[\begin{aligned} ^{L_{l}}p_{f_{i}} &= ^{L_{l}}_GR (\ ^{G}_{I_{l+1}}R\ ^{I}_{L}R\ ^{L_{l+1}}p_{f_{i}} +^Gp_{L_{l+1}} - ^Gp_{L_{l}}) \\ \end{aligned}\]然后有
\[\begin{aligned} ^Gp_{L_{l+1}} &= ^{G}_{I_{l+1}}R \ ^Ip_{L} + ^Gp_{I_{l+1}} \\ &= ^{G}_{I_{l+1}}R (- ^{I}_{L}R ^Lp_I) + ^Gp_{I_{l+1}} \\ &= -^{G}_{L_{l+1}}R\ ^Lp_{I} + ^Gp_{I_{l+1}}\\ ^Gp_{L_{l}} &= ^{G}_{I_{l}}R \ ^Ip_{L} + ^Gp_{I_l} \\ &= -^{G}_{L_{l}}R\ ^Lp_{I} + ^Gp_{I_{l}}\\ ^{L_{l}}_{G}R &=\ ^{L}_{I} R \ ^{I_{l}}_GR \\ \end{aligned}\]带入,有
\[\begin{aligned} ^{L_{l}}p_{f_{i}} &= \ ^{L}_{I} R \ ^{I_{l}}_GR (\ ^{G}_{I_{l+1}}R\ ^{I}_{L}R\ ^{L_{l+1}}p_{fi} -^{G}_{L_{l+1}}R\ ^Lp_{I} + ^Gp_{I_{l+1}}-(-^{G}_{L_{l}}R\ ^Lp_{I} + ^Gp_{I_{l}})) \\ &= \ ^{L}_{I} R \ ^{I_{l}}_GR \ ^{G}_{I_{l+1}}R\ ^{I}_{L}R\ ^{L_{l+1}}p_{fi} - \ ^{L}_{I} R \ ^{I_{l}}_GR ^{G}_{I_{l+1}}R\ ^{I}_{L}R\ ^Lp_{I} + \ ^{L}_{I} R \ ^{I_{l}}_GR ^Gp_{I_{l+1}} + ^Lp_{I} - \ ^{L}_{I} R \ ^{I_{l}}_GR ^Gp_{I_{l}} \\ \end{aligned}\]那么
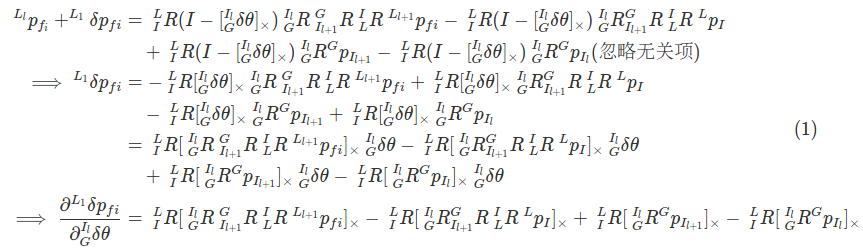
根据叉乘的性质,这个结果与论文中的公式是一样的。
剩下的雅克比就很好推了。 \(\frac{\partial ^{L_1}\delta p_{fi}}{\partial ^G \delta p_{I_{l}}} = - \ ^{L}_{I} R \ ^{I_{l}}_GR \tag{2}\)
\[\frac{\partial ^{L_1}\delta p_{fi}}{\partial ^G \delta p_{I_{l+1}}} = \ ^{L}_{I} R \ ^{I_{l}}_GR \tag{4}\] \[\frac{\partial ^{L_1}\delta p_{fi}}{\partial ^L \delta p_I} = -^{L_l}_{L_{l+1}}R + I_{3\times 3} \tag{6}\]