问题提出
在做课题时遇到了一个问题:在视觉里程计中,当平移量t较小的时候的,根据对极约束算出来的旋转矩阵R为何不可信?
背景
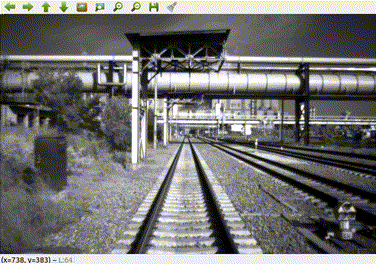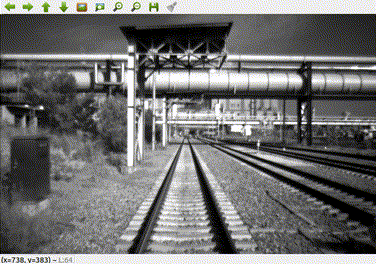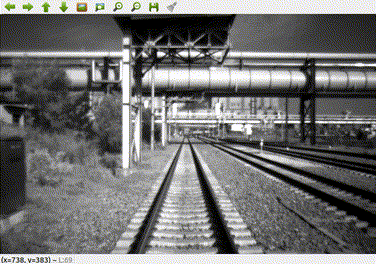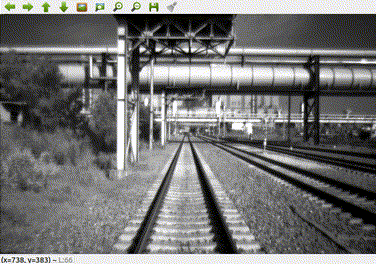
上图是录制的bag中灰度相机拍摄的图像。相机位于火车头前部,由于火车移速缓慢,导致其两帧之间的平移量t相对较小,这时通过计算本质矩阵,然后分解得出的R就相当不可信了。下图为我根据其本质矩阵分解出的R,t画的轨迹图(由于火车匀速行驶,故假设火车两帧之间的运动的尺度相等)。
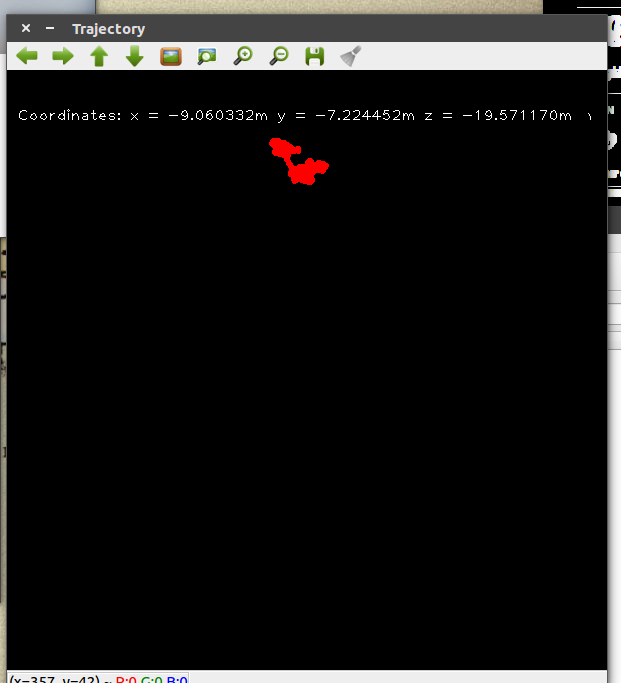
如果是正常的情况,因为火车在铁轨上运行,其轨迹应当为一直线,然而绘制出来的轨迹几乎是一团浆糊,其原因就是因为平移量过小,由本质矩阵分解出来的R是不可信的,不能直接用来绘制轨迹。
简单的视觉里程计
一个简单的单目视觉里程计的框图(参阅冯兵的博客):
graph TD;
接收图像-->提取特征点
提取特征点-->特征匹配
特征匹配-->计算本质矩阵,得到R,T
现在假设我们已得到了上一帧与这一帧相对应的像素点,如何求得上一帧相机到这一帧的R,t呢?
对极约束
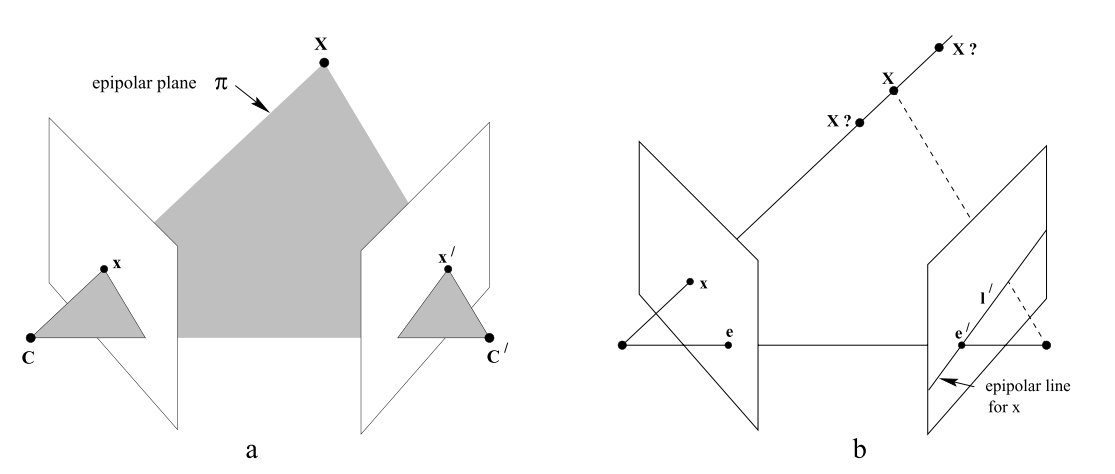
这里我们省去繁杂的推导,只需知道,如图a所示,对于空间点X,其在k时刻在相机平面上的投影为点x,在k+1时刻在相机平面上的投影为x’,并且设k+1时刻相机相对于k时刻的坐标变换用R,t表示,则对极约束可以表示成:
\(x'^{T}Fx=0\) 或者 \(p_2^{T}Ep_1= 0 \tag{1}\)
其中$p_2$,$p_1$为空间点P在两个像素坐标系中,以光心为原点的,投影到(z=1)归一化坐标(即深度z恒为1)。这部分的推导可以参阅高翔的《视觉SLAM十四讲》。
上式的$E$就被叫做本质矩阵(essential matrix),并且 \(E=\hat{t}R \tag{2}\) 将E进行奇异值分解就可以得到R,t。
本质矩阵的尺度等价性
由式1可以看出,等式两边同时乘以$\lambda$,等式依然成立。也就是说本质矩阵的自身乘以常数后仍为该方程的一个解。而式2中,由于旋转矩阵R本身的约束,导致其行列式恒为1,则对本质矩阵的缩放实质上是作用在了t身上。也就是说,根据本质矩阵求出来的t只有方向具有意义,而其大小没有意义(因为乘以常数后对极约束仍满足)。
也正是因为这个性质,导致了当两帧之间的位移量t较小或者两帧之间是纯旋转时,用本质矩阵求解的R是不可靠的。
纯旋转的情况:
此时, t为0,由式2导致E=0,式1恒成立,此时无法对E进行SVD分解。
位移量较小的情况:
由于实际情况中,不太可能有纯旋转的情况,往往是偏移量$t=(\Delta x, \Delta y, \Delta z)$。这三个小量可以看做是均值为0的正太分布,从而导致这个偏移量t的方向是随机的(而当偏移量较大时,小量相对于真正的偏移可以忽略不计,t的方向较为固定),那么分解E得到的R也具有极大的随机性,用这个R作为旋转量绘制轨迹就会出错。
解决方法
单目并且不知道两帧之间的尺度的话,可以用单应矩阵来估计旋转,也可以不计算两两帧之间的本质矩阵,而是去估算每6帧之间的本质矩阵(因为t足够大):

上图是我估计每六帧之间的R,t时绘制出来的轨迹,可以看到,一段时间内的轨迹均为直线。当然,由于我没有后端优化,所以当某一帧估计错误后,后面的轨迹会跟着继续,这也就是轨迹中折线部分的由来。