矩阵的二范数为何等于其奇异值

背景

上《线性系统理论》这门课，提到了矩阵的二范数，即等式： \(\|\mathbf{A}\|_{2}=\sqrt{\lambda_{\max }}\) 然后中文搜了一堆，没有系统地说明怎么得到的。最后在Wikipedia¹中找到了详细推导的来源，也就是这本书²中找到了详细的推导。故记录如下。

Frobenius Matrix Norm 与 Induced Matrix Norms

Frobenius Matrix Norm

Frobenius Matrix Norm简称F范数，就是课堂上讲的，其定义为： \(\|\mathbf{A}\|_{F}^{2}=\sum_{i, j}\left|a_{i j}\right|^{2}=\sum_{i}\left\|\mathbf{A}_{i *}\right\|_{2}^{2}=\sum_{j}\left\|\mathbf{A}_{* j}\right\|_{2}^{2}=\operatorname{trace}\left(\mathbf{A}^{*} \mathbf{A}\right)\) 然而由F范数的定义是推不出来 \(\|\mathbf{A}\|_{2}=\sqrt{\lambda_{\max }}\) 的，它是由Induced Matrix Norms（诱导范数）推导来的。

Induced Matrix Norms

诱导范数实际上是说，矩阵的范数是由向量的范数“诱导”来。诱导范数的定义为 \(\|\mathbf{A}\|=\max _{\|\mathbf{x}\|=1}\|\mathbf{A} \mathbf{x}\| \quad \text { for } \mathbf{A} \in \mathcal{C}^{m \times n}, \quad \mathbf{x} \in \mathcal{C}^{n \times 1}\)

用图来说明诱导范数的几何意义。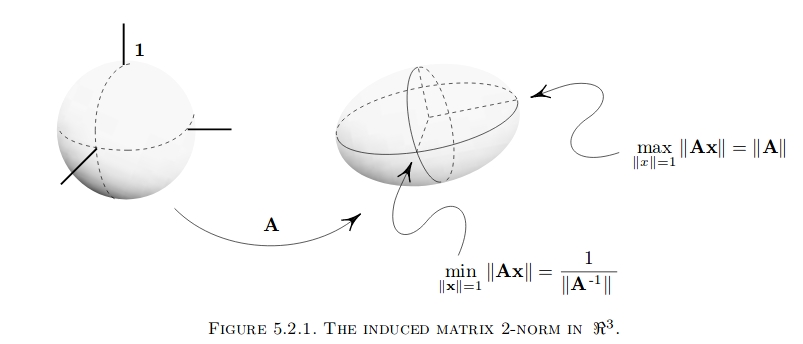

假设x为三维向量，其模长为1， 则其在坐标系中的可能位置所构成的形状如图左，为一个球形。而Ax则将左图中的球形拉扯成一个椭球形（为什么是椭球形，因为Ax的值随着x的值连续变化而连续变化，并且保持对称性），这个椭球形的最长的半径为诱导范数的值。

显而易见的，当$||x||^2_2=1$有 \(\|\mathbf{A x}\|_{2}^{2}=\sum_{i}\left|\mathbf{A}_{i * \mathbf{x}}\right|^{2} \leq \sum_{i}\left\|\mathbf{A}_{i *}\right\|_{2}^{2}\|\mathbf{x}\|_{2}^{2}=\|\mathbf{A}\|_{F}^{2}\|\mathbf{x}\|_{2}^{2}=\|\mathbf{A}\|_{F}^{2}\) 从而F范数与诱导范数的值是相等的，只是定义方式不同。

推导公式

下证 \(\|\mathbf{A}\|_{2}=\sqrt{\lambda_{\max }}\) 因为²上介绍矩阵范数时还没讲到矩阵的特征值，因此推导的有点绕，此处证明采用知乎白如冰大神的推导方式³：

因为 \(||Ax|| =\sqrt{(A x)^{T}(A x)}=\sqrt{x^{T} A^{T} A x}\) 并且$A^TA$是半正定矩阵（因为$x^{T} A^{T} A x \ge 0$）,特征值满足$\lambda_{1} \geq \cdots \geq \lambda_{n} \geq 0$，相应的特征向量$\alpha_{1}, \dots \alpha_{n}$构成$R^n$的一组标准正交基，那么设$x=\sum_{i=1}^{n} k_{i} \alpha_{i}$,因为x的模为1，所以有$\sum_{i=1}^{n} k_{i}^{2}=1$

则 \(A^{T} A x=A^{T} A\left(\sum_{i=1}^{n} k_{i} \alpha_{i}\right)=\sum_{i=1}^{n} k_{i} A^{T} A \alpha_{i}=\sum_{i=1}^{n} \lambda_{i} k_{i} \alpha_{i}\)

\[x^{T} A^{T} A x=\sum_{i=1}^{n} \lambda_{i} k_{i}^{2} \leq \lambda_{1}\]

其中$\lambda_1$为$A^TA$的最大的特征根，可知$\sqrt{(A x)^{T}(A x)} \leq \sqrt{\lambda_{1}}$，即$A^TA$的最大特征值的平方根，即$A$的最大奇异值。