如何计算ICP得到的位姿不确定性（covariance）?

背景

当使用ICP做点云配准的时候，如何评估配准结果的不确定性(亦即得到的Transform的协方差)？

hdl-graph-slam的做法

hdl 计算的不是covariance 而是信息矩阵。

在得到某个配准方法得到的transfrom后，首先根据这个transform计算这两个点云的fitness score。具体做法为：

将cloud2根据transform 变换得到cloud3。
对于cloud3里点云的每一个点，在cloud1里面找与其最近的一个点，如果这两个点的距离小于某个阈值，则fitness score += 这两个点的距离。
fitness score /= 总共的点的数量。

直观的讲，最后求得的fitness score实际上是匹配点之间的平均距离，是能够比较好的反应不确定性的。

得到fitness score 就可以计算信息矩阵的其他参数了。首先，hdl_graph_slam给了几个先验参数，比如

min_stddev_x = nh.param<double>("min_stddev_x", 0.1); // 位置标准差最小值
max_stddev_x = nh.param<double>("max_stddev_x", 5.0); // 位置标准差最大值
min_stddev_q = nh.param<double>("min_stddev_q", 0.05); // 旋转标准差最小值
max_stddev_q = nh.param<double>("max_stddev_q", 0.2); // 旋转标准差最大值

有了标准差，其平方即为方差。

先用fitness score 计算一个ratio, 配准后得到的位姿的位置的方差即为这个ratio 来决定。具体如下面两个式子决定。

\[ratio(x) = \frac{1- \exp(-a * x)} { 1- \exp(-a * max_x)} \\ weight(x) = minY + (maxY - minY) * ratio;\]

其中，上述的minY为位置的方差最小值，maxY为位置的方差最大值。

旋转的不确定性也是通过类似方法确定。

蒙特卡洛法

这个算法也挺有意思，他是在文献2中被提出的，主要流程为

假设要配准的是$y_{t-1}$帧点云与$y_t$帧点云，先读入点云$y_{t-1}$以及他前面与后面几帧的点云，组成一个局部的submap。
将$y_t$与$y_{t-1}$的点云进行配准，获得一个初始位姿$T$
以下步骤重复100次：
1. 选择一个随机的扰动加到$T$上，得到$\bar{T}$
2. 根据光线投射的原理，计算在$\bar T$的位姿上，由submap能得到的虚拟点云$\bar y_t$。
3. 配准$y_{t-1}$与$\bar y_t$，并且保存配准误差。
通过这些配准误差来计算协方差矩阵。

NDT的做法

NDT是计算其目标函数的Hessian矩阵的逆的特征值，如果其特征值都比较小，则认为其得到的位姿的不确定性也比较小。通常取他的状态的六个特征值的最大值作为一个位姿不确定性的评估。

closed-form estimate

这个就是论文[1]里提到的方法。

隐函数定理

在介绍这个方法前，先介绍一个隐函数定理：

隐函数：是形式如$f(x_1, x_2, x_3, …) = 0$的函数

隐函数定理说明，对于一个由关系 f(x, y)=0 表示的隐函数，如果它在某一点的偏微分满足某些条件，则在这点有邻域使得在该邻域內 y 可以表示成关于 x 的函数： y=f(x)

例子 :

以维基百科的例子来说。单位圆的函数为$F(x, y) = x^2 + y^2 - 1 = 0$，其图像函数为：

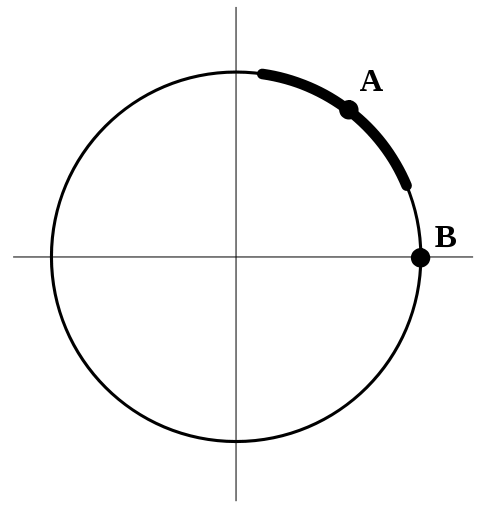
则很显然，在点A的邻域附近，x与y的显函数关系为 $y = f(x) = \sqrt{1-x^2}$

现在对原本的隐函数，对于x求全导数。

\[\begin{aligned} \frac{d F(x, y)}{d x} &= \frac{\partial F(x, f(x))}{\partial x} + \frac{\partial F(x, f(x))}{\partial y} * \frac{\partial f(x)}{\partial x} = 0 \\ \implies \frac{\partial f(x)}{\partial x} &= \frac{-\frac{\partial F(x, f(x))}{\partial(x)}}{\frac{\partial F(x, f(x))}{\partial y} } \end{aligned} \tag{1}\]

再举个例子，考虑机器人模型下的状态$x$是依赖于观测$z$的函数，即 $x = A(z) = \argmin_xJ(z,x)$ 其中J是定位问题中的某个目标函数。

现在我想求$\frac{\partial A(z)}{\partial (x)}$，那么令公式1中$F=\frac{\partial J}{\partial x}, f(z) = A(z)$,就有

\[\left.\frac{\partial A(\boldsymbol{z})}{\partial \boldsymbol{z}}\right|_{\boldsymbol{z}=\dot{z}}=\left.\left(\frac{\partial^{2} J}{\partial \boldsymbol{x}^{2}}\right)^{-1} \frac{\partial^{2} J}{\partial \boldsymbol{z} \partial \boldsymbol{x}}\right|_{\boldsymbol{x}=A(\overline{\boldsymbol{z}})}\]

ICP 方法的不确定性的close-form estimate

最传统的ICP里面的目标函数为

\[A(Z) = \argmin_x J= \argmin_x\sum_{i=1}^{n}\left\|\mathbf{R} \mathbf{P}_{\mathbf{i}}+\mathbf{T}-\mathbf{Q}_{\mathbf{i}}\right\|^{2}\]

其中$P_i$是source pointcloud 中的点，$Q_i$是target pointcloud中的点。机器人的状态变量表示为(x, y, z, a, b, c)。 a, b, c分别表示yaw pitch roll。

那么以这种方法求出来的协方差为 $\begin{aligned} \operatorname{cov}(\mathbf{x})&=\operatorname{cov}\left(\left.A(\mathbf{z})\right|_{\mathbf{z}=\mathbf{z}_{o}}\right) \approx \frac{\partial A}{\partial \mathbf{z}_{o}} \operatorname{cov}(\mathbf{z}) \frac{\partial A}{\partial \mathbf{z}_{o}}^{T} \\ &= \left(\frac{\partial^{2} J}{\partial \mathbf{x}^{2}}\right)^{-1}\left(\frac{\partial^{2} J}{\partial \mathbf{z} \partial \mathbf{x}}\right) \operatorname{cov}(\mathbf{z})\left(\frac{\partial^{2} J}{\partial \mathbf{z} \partial \mathbf{x}}\right)^{T}\left(\frac{\partial^{2} J}{\partial \mathbf{x}^{2}}\right)^{-1} \\ \end{aligned}$

计算 $\frac{\partial^2{J}}{\partial x^2}$

有 \(\frac{\partial^2{J}}{\partial x^2} = \left[\begin{array}{l} \left(\frac{\partial^{2} J}{\partial x^{2}}\right)\left(\frac{\partial^{2} J}{\partial y \partial x}\right)\left(\frac{\partial^{2} J}{\partial z \partial x}\right)\left(\frac{\partial^{2} J}{\partial \alpha \partial x}\right)\left(\frac{\partial^{2} J}{\partial b \partial x}\right)\left(\frac{\partial^{2} J}{\partial c \partial x}\right) \\ \left(\frac{\partial^{2} J}{\partial x \partial y}\right)\left(\frac{\partial^{2} J}{\partial y^{2}}\right)\left(\frac{\partial^{2} J}{\partial z \partial y}\right)\left(\frac{\partial^{2} J}{\partial a \partial y}\right)\left(\frac{\partial^{2} J}{\partial b \partial y}\right)\left(\frac{\partial^{2} J}{\partial c \partial y}\right) \\ \left(\frac{\partial^{2} J}{\partial x \partial z}\right)\left(\frac{\partial^{2} J}{\partial y \partial z}\right)\left(\frac{\partial^{2} J}{\partial z^{2}}\right)\left(\frac{\partial^{2} J}{\partial a \partial z}\right)\left(\frac{\partial^{2} J}{\partial b \partial z}\right)\left(\frac{\partial^{2} J}{\partial \operatorname{cog} z}\right) \\ \left(\frac{\partial^{2} J}{\partial x \partial a}\right)\left(\frac{\partial^{2} J}{\partial y \partial a}\right)\left(\frac{\partial^{2} J}{\partial z \partial a}\right)\left(\frac{\partial^{2} J}{\partial a^{2}}\right)\left(\frac{\partial^{2} J}{\partial b \partial a}\right)\left(\frac{\partial^{2} J}{\partial c \partial a}\right) \\ \left(\frac{\partial^{2} J}{\partial x \partial b}\right)\left(\frac{\partial^{2} J}{\partial y \partial b}\right)\left(\frac{\partial^{2} J}{\partial z \partial b}\right)\left(\frac{\partial^{2} J}{\partial a \partial b}\right)\left(\frac{\partial^{2} J}{\partial b^{2}}\right)\left(\frac{\partial^{2} J}{\partial c \partial b}\right) \\ \left(\frac{\partial^{2} J}{\partial x \partial c}\right)\left(\frac{\partial^{2} J}{\partial y \partial c}\right)\left(\frac{\partial^{2} J}{\partial z \partial c}\right)\left(\frac{\partial^{2} J}{\partial a \partial c}\right)\left(\frac{\partial^{2} J}{\partial b \partial c}\right)\left(\frac{\partial^{2} J}{\partial c^{2}}\right) \end{array}\right]\)

因为 $J=\sum_{i=1}^{n}\left\|\mathbf{R} \mathbf{P}_{\mathbf{i}}+\mathbf{T}-\mathbf{Q}_{\mathbf{i}}\right\|^{2}$ 将其改写为 $J = \sum^n_{i=1} F^2$ 其中$F= ||G||$，$G=RP_i+T-Q_i$;

那么，对于一组匹配而言有 $\begin{aligned} &\frac{\partial J_{i}}{\partial x}=2 \cdot F \cdot \frac{\partial F}{\partial x} \\ &\frac{\partial F}{\partial x}=\frac{J_{G}(x)^{T} \cdot G}{\|G\|} \\ & J_{G}(x)=\frac{\partial G}{\partial x}=\frac{\partial}{\partial x}\left(\mathbf{R} \mathbf{P}_{\mathbf{i}}+\mathbf{T}-\mathbf{Q}_{\mathbf{i}}\right) \end{aligned}$ 再将公式继续展开就可以得到一组匹配的偏导。将所有的匹配的偏导求出来再求和即得到了这一项。

计算$\frac{\partial^2 {J}}{\partial{z}\partial{x}}$

其实和之前的差不多，就是分子变成了对$P_i，Q_i$求偏导。

计算$cov(z)$

这个就是一个传感器噪声了，为自己的一个设置的值，形式为

\[J_{G}(x)=\frac{\partial G}{\partial x}=\frac{\partial}{\partial x}\left(\mathbf{R} \mathbf{P}_{\mathbf{i}}+\mathbf{T}-\mathbf{Q}_{\mathbf{i}}\right)\]

参考论文

Prakhya, Sai Manoj, et al. “A closed-form estimate of 3D ICP covariance.” 2015 14th IAPR International Conference on Machine Vision Applications (MVA). IEEE, 2015.A Closed-form Estimate of 3D ICP Covariance Prakhya
O. Bengtsson, Robust Self-Localization of Mobile Robots in Dynamic Environments Using Scan Matching Algorithms. PhD thesis, Depart- ment of Computer Science and Engineering, Chalmers University of Technology, Göteborg, Sweden, 2006. ISBN 91-7291-744-X.

上篇如何用CUDA加速并行你的程序（以八叉树光线投射为例）